Efficient algorithms for parametric system identification with application to temperature control

Léo Simpson, Tool-Temp AG

My research focuses on implementing a Model Predictive Control (MPC) scheme for temperature regulation within a Temperature Control Unit (TCU). Central to this task are precise predictive models of temperature behavior, developed using a combination of physics-based knowledge and experimental data. Given that system components may change over time, parametric system identification is crucial for integrating physics-based insights and adapting models to new data. 

Considering that other control applications might also benefit from general tools for parametric system identification, the primary aim of my research shifted toward the development of efficient and reliable algorithms for parametric system identification.

Nevertheless, temperature control remains a key motivation. Consequently, I am also working on implementing a learning-based MPC scheme for TCUs.

Efficient Parametric System Identification

[1] Simpson, Ghezzi, Asprion, Diehl, “An Efficient Method for the Joint Estimation of System Parameters and Noise Covariances for Linear Time-Variant Systems” – CDC 2023

[2] Simpson, Asprion, Muntwiler, Köhler, Diehl, “Parallelizable Parametric Nonlinear System Identification via tuning of a Moving Horizon State Estimator” – submitted for CDC 2024

In my research, I focus on parametric system identification, where a model based on physical principles is provided, but some parameters are unknown. The goal is to estimate these parameters using experimental data. Unlike non-parametric methods such as Subspace methods, Gaussian Processes, or deep Neural Networks, parametric methods benefit significantly from incorporating prior knowledge.

A robust and versatile framework for this task is the Prediction Error Method (PEM), which minimizes the error between measured data and model-based predictions over the parameter set. However, this approach often requires solving complex nonlinear optimization problems. My research began with developing an efficient algorithm to address these challenges.

Traditionally, PEM is designed for Linear Time-Invariant (LTI) systems. In my work [1], I demonstrated the method’s versatility by extending it to Linear Time-Variant (LTV) systems and systems with nonlinear input dynamics, while maintaining theoretical guarantees. Additionally, I found that this framework allows for the joint estimation of the noise model, crucial for designing state estimators.

Furthermore, in [1], I also developed and implemented a tailored Sequential Quadratic Program (SQP) for reliably and efficiently solving the resulting nonlinear optimization problems.

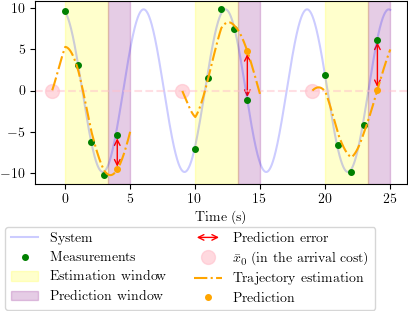
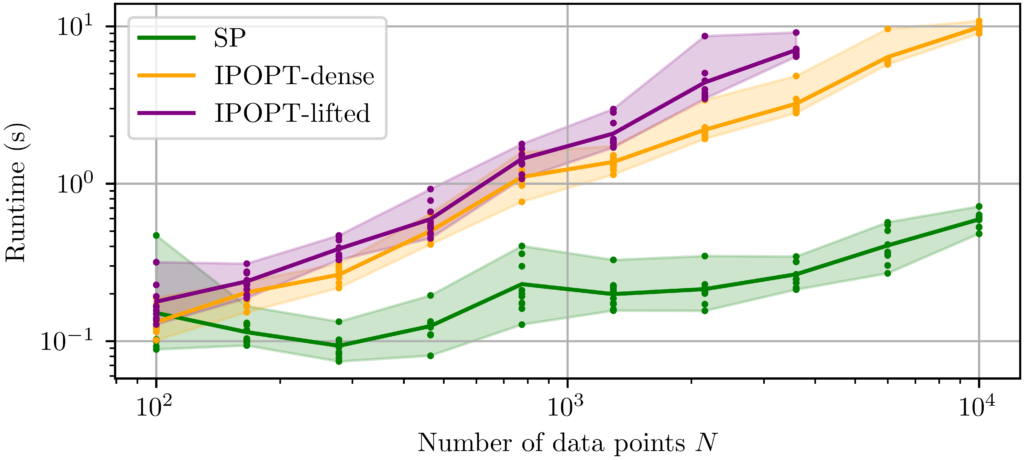
In my most recent research [2], I developed a variation of PEM for parametric nonlinear system identification using a Moving-Horizon State Estimator (MHE) for output predictions. This approach extends PEM to general parametric state-space nonlinear systems and facilitates efficient optimization. By computing output predictions using only a finite window of past data, it avoids the expensive propagation of derivatives over long data horizons. It also leaves room for parallel computation in the general case, and considerably reduces the complexity of the problem for LTI systems.

Importantly, we show this reduction in optimization complexity does not compromise the theoretical guarantees applicable to LTI systems.

In the next steps, I will design an algorithm for LTI parametric system identification, build upon the PEM variation [2], reducing the computational burden to its minimum, and guaranteeing asymptotic consistency of the estimate, even for closed-loop identification.

Checkout my open-source SysID package: MLE-LTV and MLE-LTI

Trajectory estimation (orange dashed line) using MHE with a constant arrival cost and a horizon of 4 steps and one-step-ahead prediction errors (red arrows). The system is a harmonic oscillator with discrete measurements (green dots). The MHE is computed for a model mismatch on the frequency of the oscillator.
Trajectory estimation (orange dashed line) using MHE with a constant arrival cost and a horizon of 4 steps and one-step-ahead prediction errors (red arrows). The system is a harmonic oscillator with discrete measurements (green dots). The MHE is computed for a model mismatch on the frequency of the oscillator. See [2] for more info.
Runtime of the proposed algorithm for PEM (in green) versus solving the problem with the Nonlinear Programming solver IPOPT in the lifted or condensed form (in purple and yellow). See the open-source package MLE-LTI for more info.

Learning-based Model Predictive Control for Temperature Control Units

[3] Xie*, Simpson*, Asprion, Scattolini, “A Learning-based Model Predictive Control Scheme with Application to Temperature Control Units” – CCTA 2024

* Equal contribution

This research focuses on implementing a Model Predictive Control (MPC) scheme for temperature control in Temperature Control Units (TCUs). MPC is a versatile control strategy that not only tracks desired temperature profiles but also incorporates additional objectives such as minimizing economic costs. In this study, we leverage MPC to achieve precise temperature regulation while reducing energy consumption.

The model utilized in our MPC framework is derived using parametric linear system identification, following the method developed in [1]. Additionally, we explore an alternative learning approach based on a neural network model developed by my ELO-X colleague, Jing Xie.

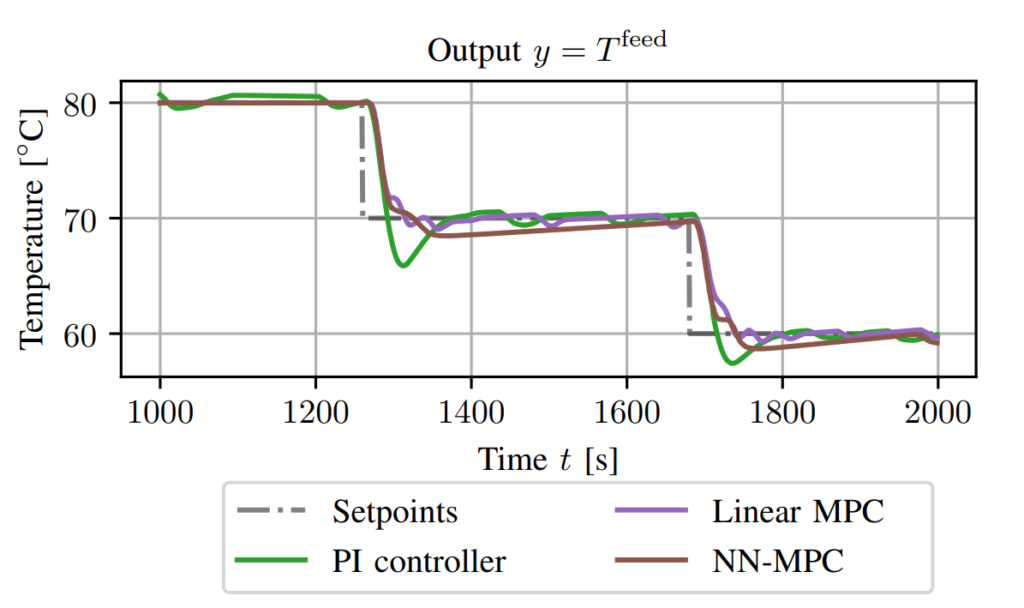
I conducted several experiments with the TCU hardware. First, to collect data for the model learning part. Then we assessed the performance of the controllers in temperature tracking experiments.

In [3], we detail the control architecture, implementation, and experimental results. The performance of the MPC controller is compared to a traditional Proportional-Integral (PI) controller, commonly used in such applications. Our findings indicate that although the PI controller is capable of tracking temperature profiles, the MPC scheme outperforms it by consuming 35% less energy. This efficiency is achieved by the MPC’s ability to avoid overshooting or undershooting the target temperatures.

Overall, the research demonstrates the potential of MPC in enhancing energy efficiency in TCUs while maintaining accurate temperature control, presenting a significant improvement over traditional PI controllers.

In the next steps, I will implement and test an adaptive MPC scheme, where the parameters are estimated online, with operating data, rather than in a separate phase.

Experiment set-up for the demonstration of the results on System Identification and Model Predictive Control for Temperature Control Units.
Temperature profiles during the three experiments: the PI controller, the MPC based on Linear System Identification,. and the MPC based on Neural-Network model learning. See [3] for more info.