Optimal Control of Switched Systems Under Dwell Time Constraints
Ramin Abbasi Esfeden, Atlas Copco Airpower
Systems with discrete inputs are common in real-world applications. However, due to the discrete nature of the inputs, solving their optimal control problem is challenging. A common approach is to first discretize the problem and then optimize it using Mixed-Integer Nonlinear Programming (MINLP) techniques. More efficient approaches involve approximating the discrete inputs. The same problem has also been investigated under the name of mode scheduling. Many of the previous approaches lose efficiency or accuracy when specific constraints, known as dwell-time constraints, are introduced. These constraints are often necessary in practical applications due to physical limitations. A common example is the minimum dwell-time constraint, which puts a lower bound on the duration between two switchings of the discrete input.
Iterative Switching Time Optimization for Mixed-Integer Optimal Control Problems
This research proposes an iterative method to solve Mixed-Integer Optimal Control Problems arising from systems with switched dynamics. The so-called relaxed problem plays a central role within this context. Through a numerical example, it is shown why relying on the relaxed problem can lead the solution astray. As an alternative, an iterative Switching Time optimization method is proposed. The method consists of two components that iteratively interact: a Switching Time optimization (STO) problem and a sequence optimization. Each component is explained in detail, and the numerical example is resolved, the results of which show the efficiency of the proposed algorithm. Finally, the advantages and disadvantages of the method are discussed and future lines of research are sketched.

Optimal Control of Switched Systems Under Dwell Time Constraints
Discretization of dynamic systems with discrete input leads to Mixed-Integer Nonlinear Programming, which is a challenging problem to solve. In this project, we are looking at more efficient Mixed-Integer formulations to solve the same problem. The resulting MINLP can be solved using available software packages such as Bonmin. Numerical results show that the new formulation is orders of magnitude faster than the conventional formulation, while achieving similar performance. The results are also compared to the previously developed Iterative Switching Time Optimization algorithm and other approximation methods such as CIA.
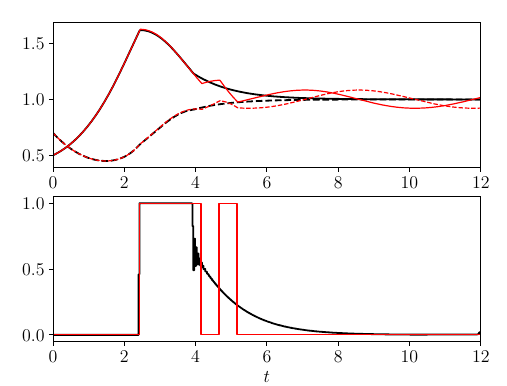
The figure shows the optimal solution to the Lotka-Volterra Fishing optimization problem. The Lotka Volterra fishing problem is a Mixed Integer Optimal Control Problem (MIOCP) that finds a fishing strategy (bottom), in terms of allowing fishing or not, over 12 years to control the predator-prey fish to a sustainable steady-state value (top). The black line shows the relaxed solution, and the red line shows the optimum solution we are seeking. In this example, there is a minimum dwell time constraint of 6 months on our decision.