Algorithms for solving nonlinear programs
Lahcen El Bourkhissi, Polytechnic University of Bucharest
In my research, I focus on addressing nonlinear programs, which commonly arise in Nonlinear Model Predictive Control and other areas like machine learning. Solving these problems is challenging due to their nonconvex and sometimes nonsmooth nature. My primary goal is to develop efficient methods based on penalty and augmented Lagrangian approaches capable of effectively handling such challenges. Specifically, I aim to devise methods that involve solving only simple subproblems, such as convex subproblems.
Penalty-based method for solving nonlinear programs
[1] El Bourkhissi, Necoara “Complexity of linearized quadratic penalty for optimization with nonlinear equality constraints” – submitted, 2023
IN [1], we considered a nonconvex optimization problem with nonlinear equality constraints. We assumed that both the objective function and the functional constraints were locally smooth. To solve this problem, we applied a linearized quadratic penalty method. That is, we linearized the objective function and the functional constraints in the penalty formulation at the current iterate and added a quadratic regularization, thus yielding a subproblem that is easy to solve (in fact, the solution of our subproblem is equiavlent to the solving a linear system), and whose solution was the next iterate. Under a dynamic regularization parameter choice, we derived convergence guarantees for the iterates of our method to an ε first-order optimal solution in O(1/ε^3) evaluations of the first order information of the objective function and functional constraints. Finally, we showed that when the problem data satisfied the Kurdyka-Lojasiewicz property, e.g., were semialgebraic, the whole sequence generated by our algorithm converged and we derived convergence rates. We validated the theory and the performance of the proposed algorithm by numerically comparing it with some existing methods from the literature.
ADMM scheme for nonsmooth nonlinear programs
[2] El Bourkhissi, Necoara, Patrinos, “Linearized ADMM for nonsmooth nonconvex optimization with nonlinear equality constraints”, CDC 2023
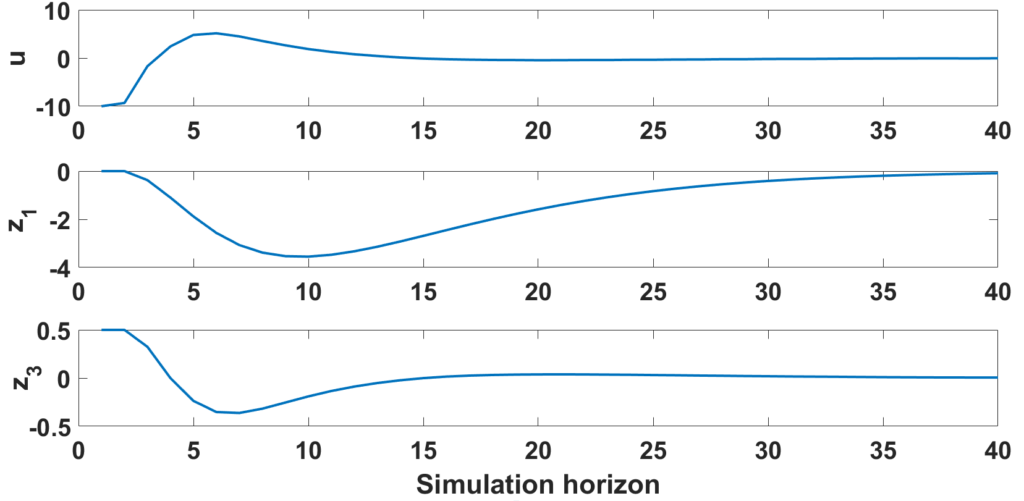
In [2], we proposed a new approach for solving a structured nonsmooth nonconvex optimization problem with nonlinear equality constraints, where both the objective function and constraints were 2-block separable. Our method was based on a 2-block linearized ADMM, where we linearized the smooth part of the cost function and the nonlinear term of the functional constraints in the augmented Lagrangian at each outer iteration. This resulted in simple subproblems, whose solutions were used to update the iterates of the 2 blocks variables. We proved global convergence for the sequence generated by our method to a stationary point of the original problem. We applied our proposed algorithm as a solver for the nonlinear model predictive control problem of an inverted pendulum on a cart.