Algorithms for solving hard optimization problems
Andrea Ghezzi, University of Freiburg
In my research, I focus on optimization methods and algorithms that aim to “solve” problems in different classes. All these problems share one thing, they are terribly hard to solve. On the one hand, we investigate algorithms for computing solutions of mixed-integer nonlinear programs (MINLPs), where the complexity lies in the combination of nonlinear and combinatorial optimization. On the other hand, we regard nonlinear programs (NLPs) that arise from nonlinear model predictive control (NMPC). Here the major hurdle is to solve NLPs online and on resourced-constrained hardware.
Solving mixed-integer nonlinear programs
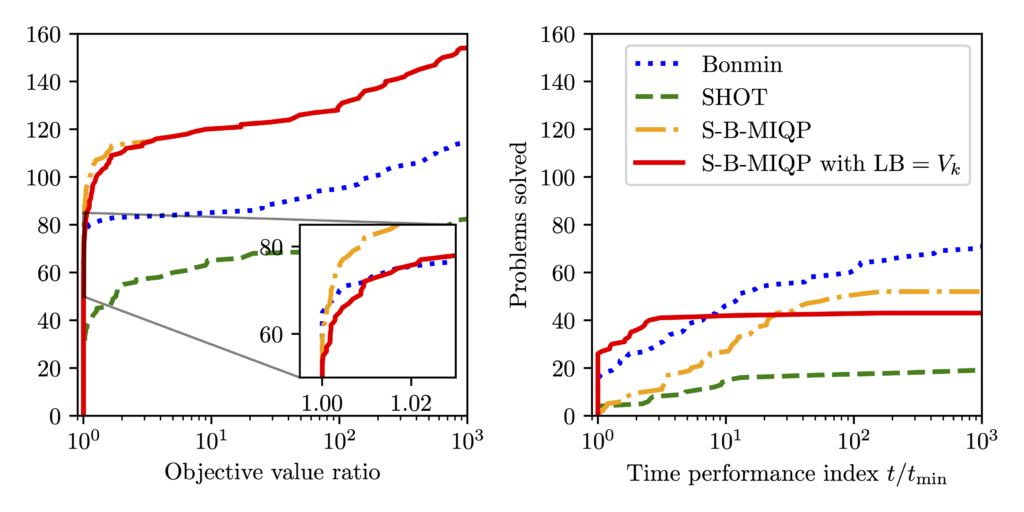
[1] Ghezzi*, Van Roy*, Sager, Diehl, “A sequential Benders-based mixed-integer quadratic programming algorithm” – submitted, 2024
[2] Ghezzi, Simpson, Bürger, Zeile, Sager, Diehl, “A Voronoi-based mixed-Integer Gauss-Newton algorithm for MINLP Arising in optimal control”, ECC 2023
* Equal contribution
For continuous decision spaces, nonlinear programs (NLPs) can be efficiently solved via sequential quadratic programming (SQP) and, more generally, sequential convex programming (SCP). These algorithms linearize only the nonlinear equality constraints and keep the outer convex structure of the problem intact. We aim to develop algorithms that extend the SQP/SCP methodology to mixed-integer nonlinear programs (MINLPs) and leverage the availability of efficient mixed-integer quadratic programming (MIQP) solvers.
Our latest algorithm, S-B-MIQP, presented in [1], is a heuristic method without any global optimality guarantee, it converges to the exact integer solution when applied to convex MINLP with a linear outer structure. The conducted numerical experiments on existing benchmarks demonstrate that the proposed algorithm is competitive with other open-source solvers for MINLP. Finally, we demonstrate via numerical simulations that the developed algorithm work out-of-the-box for mixed-integer optimal control problems (MIOCPs) transcribed into MINLPs via direct methods. These problems are characterized by numerous nonlinear equality constraints, a major hurdle for generic MINLP solvers.
Checkout our open-source MINLP toolbox package: minlp-toolbox
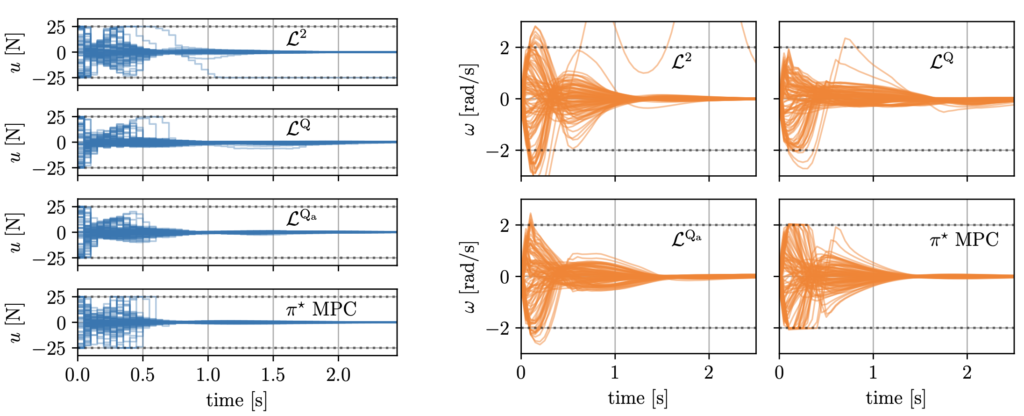
Imitation learning from nonlinear model predictive control
[3] Ghezzi*, Hoffman*, Frey, Boedecker, Diehl, “Imitation Learning from Nonlinear MPC via the Exact Q-Loss and its Gauss-Newton Approximation”, CDC 2023
* Equal contribution
We proposed a novel loss function for imitation learning from NMPC that …