Physics-informed learning for MPC in industrial applications
Next-generation embedded control systems will have to cope with tight constraints on computation and storage resources, while at the same time satisfying increasingly challenging requirements on performance quality, energy consumption, safety, emissions, etc. In this context, model-based control techniques such as MPC are envisioned to play a key role, by providing a systematic framework to minimize a desired objective function under constraints. Real application of online MPC to high-volume automotive production programs and other industrial applications has only very recently started to blossom and will likely continue to spread in the next years, but developments in the field of learning-based MPC, i.e. novel techniques nonlinear MPC incorporating machine learning techniques, is expected to accelerate the use even further.
This research project focuses on the development of novel physics-informed methods for learning and adapting prediction models for embedded nonlinear MPC. By exploiting physical knowledge in the training process learning-based components such as neural networks of rather limited size can be used to capture model mismatches. The developed algorithms aims at easing the design of MPC controllers and improve their performance, by reducing calibration time before production and adapting calibration parameters at run-time. Further, tailored optimization algorithms for solving the underlying numerical programs are investigated to enable real-time embedded applications of the proposed learning-based MPC methods.
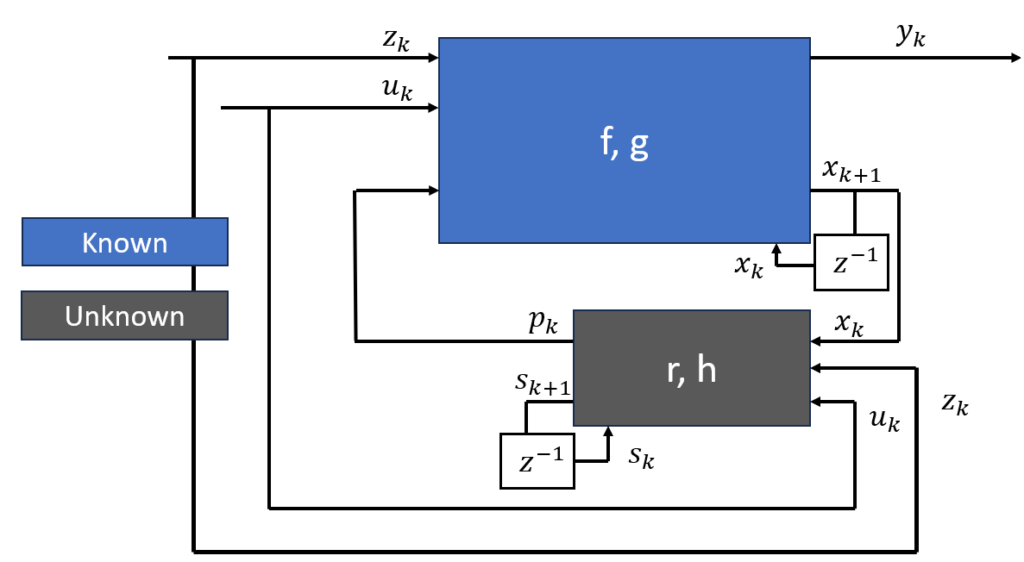
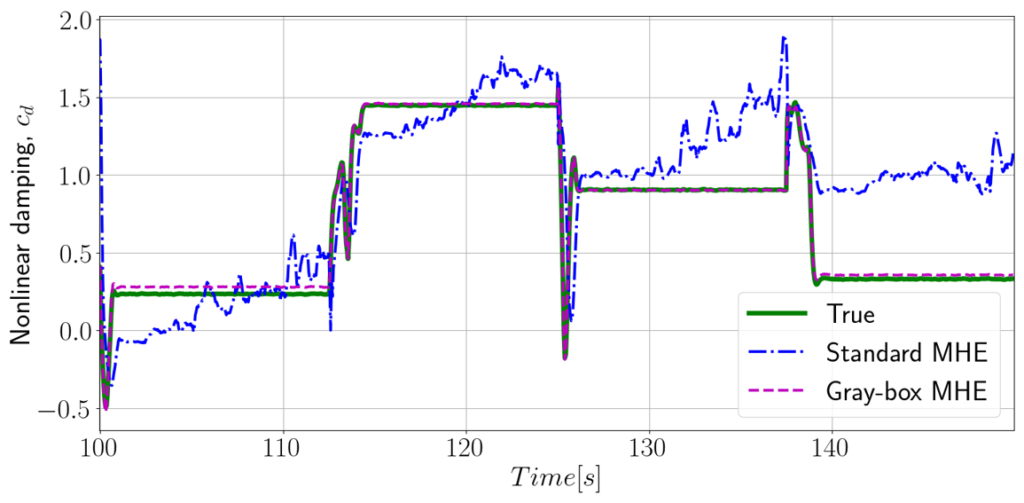
Physics-informed online learning of gray-box models by moving horizon estimation
A simple yet expressive prediction model is an essential ingredient in model-based control and esti- mation. Models derived from fundamental physical principles may fail to capture the complexity of the actual system dynamics. A potential solution is the use of a physics-informed , or gray-box model that ex- tends a physics-based model with a data-driven part. Learning the latter might be challenging, due to noisy measurements and lack of full state information. This work presents a method based on Moving Horizon Estimation (MHE) for simultaneous state estimation and training of a black-box submodel, such as a neural network. The method can be used in offline training or applied online for adaptation without any prior knowledge than the white-box submodel.
Proximal Augmented Lagrangian tailored for MPC problems
For nonlinear MPC a typical solution procedure is obtained by solving a series of constrained quadratic programs i.e., sequential quadratic programming. Therefore, a key ingredient in embedded nonlinear MPC is fast and reliable solver for the resulting quadratic subproblem. A tailored version of the Proximal Augmented Lagrangian method (QPALM) is developed to explicitly handle the equality constraints stemming from the system dynamics. The method allows for multiple active set changes while preserving a cheap inner subproblem that can be efficiently handled by semismooth Newton steps. The linear algebra is implemented to exploit the sparse structure obtained by solving the MPC in the non-condensed version a.k.a. multiple shooting.
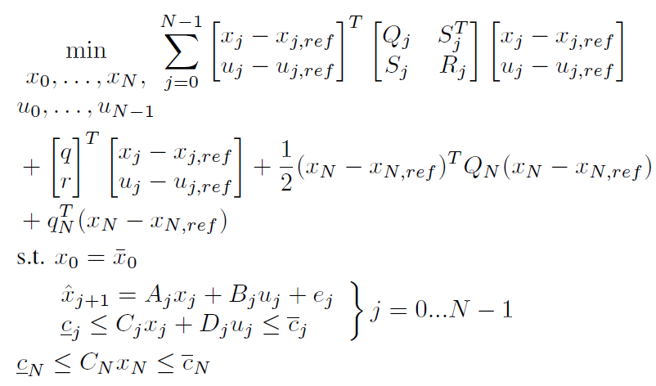
Application to industrial problems
Ongoing work in ODYS Srl.
The methods developed throughout the research project are tested with real-world data and applications from various industries mainly focusing on robotic and automotive use cases. This serves as a proof of concept of the developed methods and aims to pinpoint opportunities for further development and thereby closing the gap between theoretical research and industrial applications.

