Gain-scheduled Trajectory Tracking with Safety Guarantees
Nicolas Kessler, Politecnico di Milano
Tracking of reference trajectories is a common task in control theory. However, it tends to be challenging to design a feedback controller, if the system is nonlinear or the error dynamics during tracking exhibit different behavior. This project proposes Linear Matrix Inequality (LMI) conditions to design a gain-scheduled feedback law and proposes guarantees on robustness and safety. A major advantage of LMI conditions is the availability of well-performing solvers and due to the convexity of the set of feasible solutions, convergence of the solver is guaranteed in polynomial time. The proposed method allows for consideration of nonlinearities and constraints on the states and inputs while maintaining convexity of the solution set. Further, we extend the result to allow for a solution optimizing a quadratic performance criterion.
Tracking of fixed Reference Trajectories
We begin by considering the error dynamics along a fixed reference trajectory. The error dynamics are given by the variation of the evolution of the state under the variation of the input to the system. For each time step, the error dynamics are linearized, yielding a reference linearization and the nonlinearity of the system is considered to be an uncertainty on said reference linearization. The uncertainty itself can be bounded with a polytopic set, resulting in a Linear Difference Inclusion (LDI) for each time step.
The idea is to allow the Lyapunov function and feedback to vary along the reference trajectory and enforce, that the Lyapunov function is always decrescendant during the tracking. To stabilize an LDI with a linear feedback, well-known LMI conditions exists. These LMI conditions guarantee stability by co-designing the time-varying feedback as well as a time-varying quadratic Lyapunov function which is decrescendant for any linear system contained in the LDI.

This rendering shows a drone following a reference trajectory for take-off.
Reference Trajectories subject to Decisions
It is common that a system is supposed to follow a reference trajectory, possibly cyclic, which may be subject to a decision in the sense that in a given time step, the operator or supervisor may require the system to switch to another reference trajectories. This is a common setting in power production or industrial systems. We tackle this problem of stabilizing a set of reference trajectories by considering each state a node in a graph. If at least one trajectory connects two distinct states, we consider an edge to be present. Thus, given a set of reference trajectories, we obtain a graph of error dynamics. Recall, that above we obtained an LMI condition for tracking of a reference trajectory. Therefore, stabilizing a single edge in the above graph is representable as an LMI. Now consider the condition, that the node-dependent feedback and Lyapunov-function needs to stabilize all edges in the graph simultaneously. The resuling condition remains LMI representable, thus allowing for a fast numeric solution. In this fashion, a node-dependent, stabilizing feedback and Lyapunov function can be co-designed.
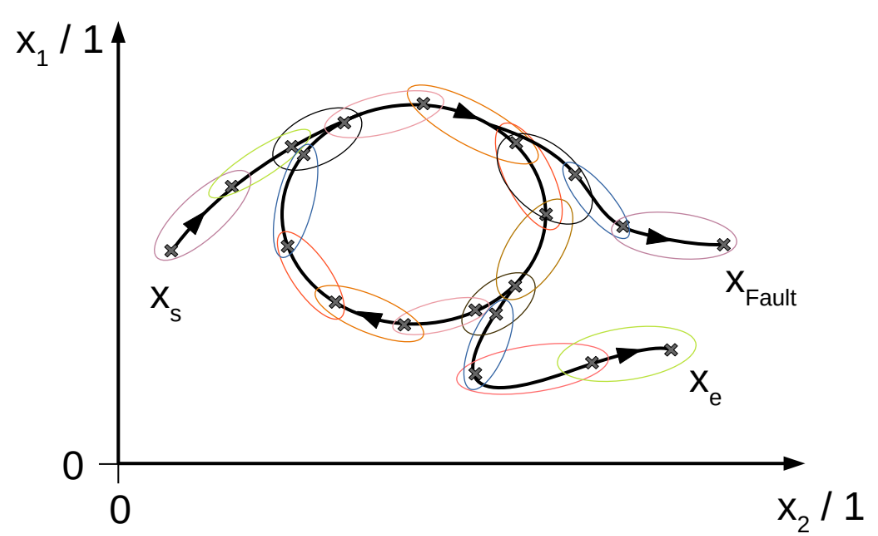
An example for a cyclic reference trajectory in phase-space with an on-ramp and two off-ramps, one for fault recovery and another to shut down the plant.
Symbolic Control
The LMI condition used to stabilize a set of reference trajectory is quite flexible. However, the set of reference trajectories may not be well-known. It is common, that one wishes to stabilize a set of reference trajectories, of which only the bounds are known. Symbolic control offers a framework to generate a graph, for which we can co-design a gain-scheduled Lyapunov function and feedback. The idea in symbolic control is to discretize the set of possible states and inputs into regions. For each region, we can formulate an uncertain linear system in the form of an LDI, that describes the system’s error dynamics, if it were to follow a reference trajectory passing the region. Then, consider the regions nodes of a graph connected by an edge, if there is a trajectory leading from one region to another. For the resulting graph, we can formulate an LMI condition as we did to stabilize a set of reference trajectories and employ a solver to find a node-dependent feedback gain.
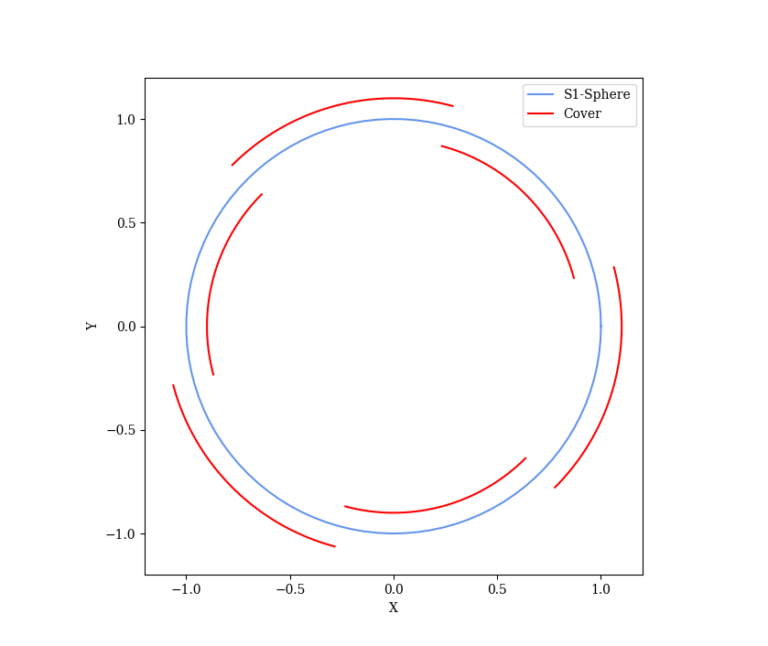
A (bounded) state corresponding to an angle (S1-sphere), commonly found in robotics, can be split into a finite number of regions. We design a feedback for each region, such that the system is stabilized within each region and during transitions to the neighboring regions.
Tube-MPC
We address performance optimization under external disturbances by extending the gain-scheduled control law to a Model Predictive Controller (MPC). In MPC, an optimal control problem is solved in each time step, where a perfomance criterion is minimized. Of the resulting solution, only the first control input is applied in a given time step and the problem is solved again in the next time step with the current value or estimate of the state.
The extended LMI condition co-designs a gain-scheduled feedback and a Lyapunov function for a given graph of error dynamics and a performance criterion, such that the Lyapunov function is an upper-bound on the performance cost at all times. In virtue of those two properties, we can consider a finite-time-horizon cost in the MPC consisting of the cost in each time step along the reference trajectory within the time horizon plus the Lyapunov function’s predicted value in the node at the end of the time horizon. This ensures, that the MPC is stabilizing: The Lyapuonov function at all times is an over-estimate of the performance cost, therefore, any tracking error at the end of the horizon is more expensive for the MPC than it is to bring the tracking error to zero.
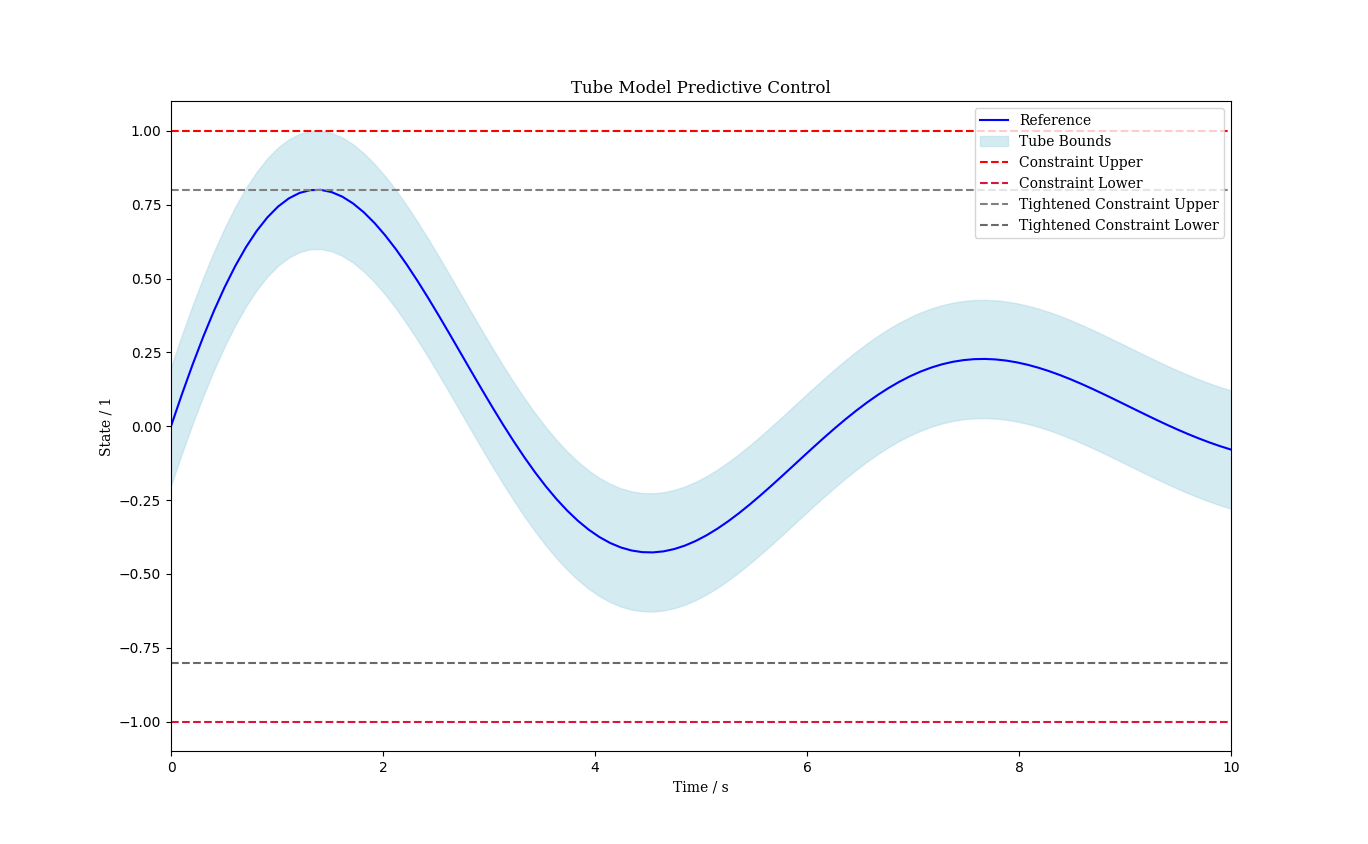
Finally, we extend the MPC to a tube-MPC to ensure safety under external disturbances by shrinking the original constraints such that the disturbance cannot nudge the system beyond them. This procedure is known as constraint tightening. As illustrated below, satisfaction of the tightened constraints ensures satisfaction of the original constraints under disturbances.
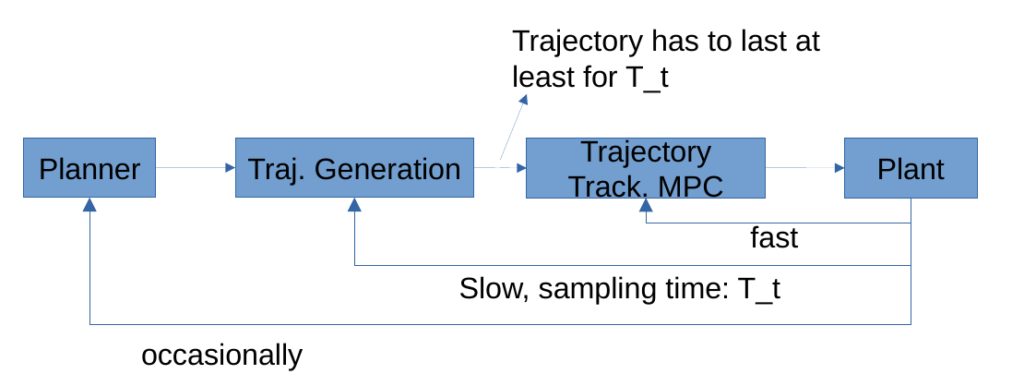
Hierarchical Control System
The proposed controller is implemented in a hierarchical manner. The trajectory tracking MPC handles stabilization along reference trajectories which are generated by a path planner or a trajectory generator. The generator gets commands from a mission planner and can employ a nonlinear MPC at lower sampling rates for trajectory generation.
Simulation Results
The gain-scheduled control law is demonstrated Continuously Stirred Tank Reactor (CSTR) which is operated in optimal steady state or periodic operation with transitions in-between these two modes. A set of trajectories has been computed offline for the modes of operations and transitions between them and the control law successfully stabilized the CSTR such that the reference trajectories are tracked. For more details on this example, please see the publication.
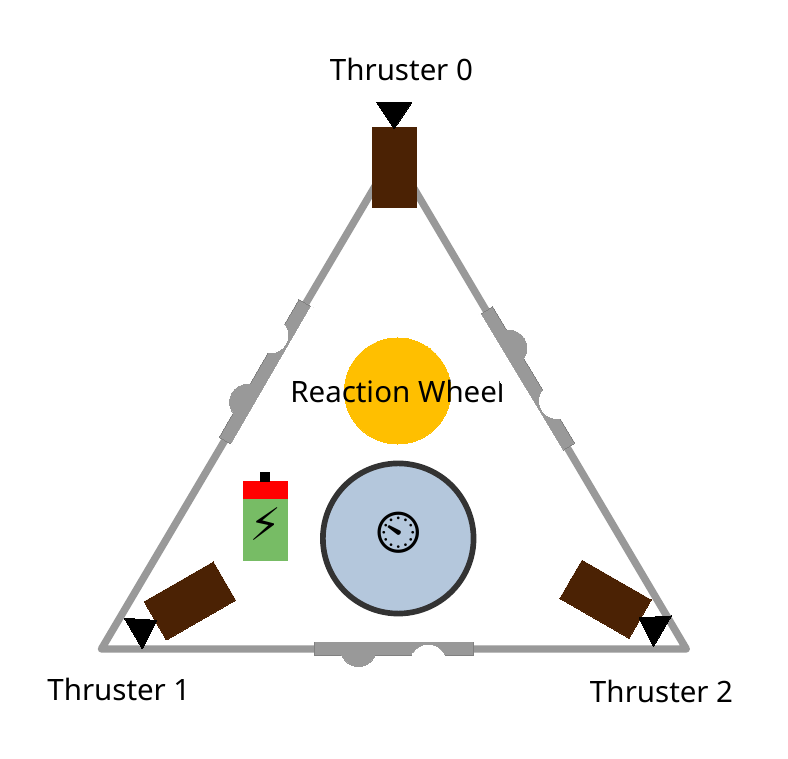
Stabilizing a set of reference trajectories of which only the bounds are known is demonstrated on a hovercraft. We generate trajectories to steer the hovercraft to the target position offline and employ the tube-MPC control law to stabilize trajectory tracking. We demonstrate, that the symbolic control approach can be applied to reasonably sized mechanical systems and that the MPC law can be run in real-time.
Implementation on a CrazyFlie Drone
The control laws are to be implemented in hardware on a CrazyFlie drone powered by an STM32F405 microcontroller. We successfully demonstrate gain-scheduled trajectory tracking on this experimental setup as well as a robust trajectory-tracking employing a tube-MPC.



