Robust offset-free tracking for systems learnt by NNARX networks
Learning algorithms for model identification and control design are increasingly popular in the control community, where large and informative data-sets are utilized to extract important information on the characteristics of the system under control.
In this project, a robust Model Predictive Control (MPC) scheme that provides offset-free setpoint tracking for systems described by Neural Nonlinear AutoRegressive eXogenous (NNARX) models. To this end, a NNARX model that learns the dynamics of the plant from input-output data is augmented with an explicit integral action on the output tracking error. A robust tube-based MPC is finally designed, to ensuren robustness. Numerical simulations on a water heating system show the effectiveness of the proposed control algorithm.
Model Identification by NNARX Networks

Neural nonlinear autoregressive exogenous (NNARX) models, where the output is computed as the nonlinear regression of the past input-output data. The nonlinear regression consists of M layers of Feed-Forward neural networks, where each layer is a linear combination of its input u, followed by a nonlinear activation function σ. The goal of the model identification is to find the best set of weights to minimize the Mean Square Error (MSE).
Controller Design
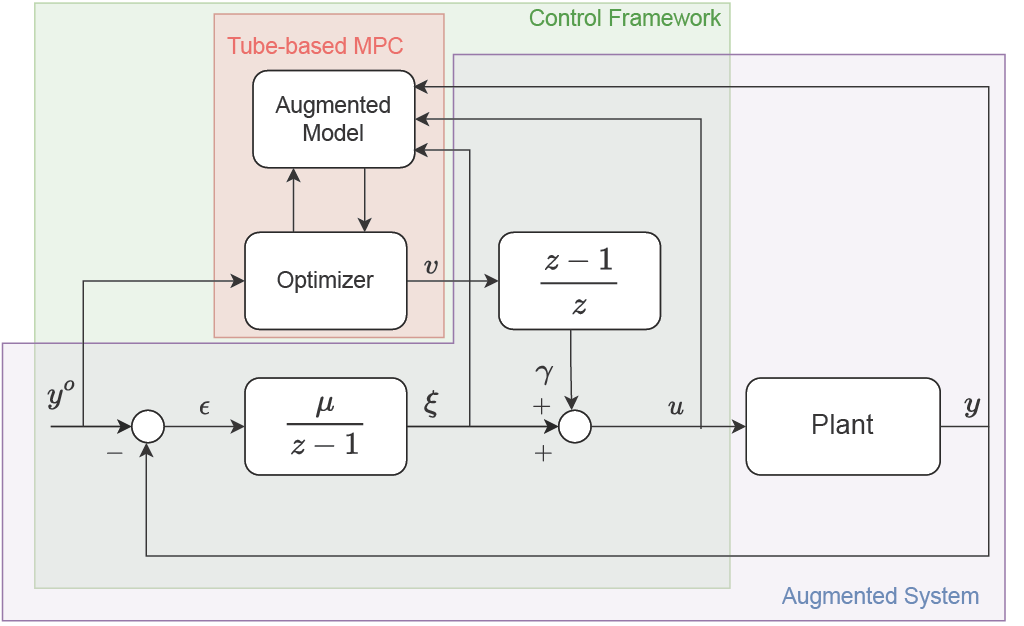
The goal of this project is to design a control system such that the controlled output tracks a given constant reference signal y in a robust way. The proposed control scheme is shown in the left figure. The regulator is made of three main blocks: an integrator of the output tracking error, an MPC algorithm, and a derivative action.
1. The integrator acts on the output tracking error so that, in light of the Internal Model Principle, it is ensured that error converges to zero.
2. The MPC algorithm provides improved performances in transient conditions and the fulfillment of input and output constraints, while at the steady state, its action is null due to the derivative action acting on its output. In addition, a tube is designed to ensure robustness in the presence of disturbance.
3. The derivative action allows to achieve stability results for the overall system by means of a standard zero terminal constraint formulation of MPC.
Simulation

A water-heating benchmark system is used to test the proposed control framework. The goal of the system is to regulate the temperature of the outlet water to a desired value with the required flow rate. The simulation results show the proposed approach achieves zero-error tracking performance and guarantees robustness in the presense of asymptotically constant disturbance.
For more details, please see the publication.

